Wprowadzenie

Tworzenie własnych klas

Uruchamianie zewnętrznych procesów

Konsola “ipython”

Tworzenie własnych generatorów

Tworzenie własnych modułów

Instalacja OpenFOAM i ParaView

Do rozwiązania poniższego zadania będzie wymagane zainstalowanie aplikacji OpenFOAM. OpenFOAM jest zbiorem różnych solverów opensource, które pozwalają na rozwiązywanie zagadnień obliczeniowej mechaniki płynów. W przypadku naszego zadania będzie on zastosowany do tworzenia siatki i wykonania obliczeń przepływu 2D, których wynik będzie następnie przez nas wykorzystany do utworzenia optymalizacji. Instalacja OpenFOAM z pakietów jest bardzo prosta. Opis instalacji można znaleźć pod tym linkiem. Poniżej opisujemy dokładnie te same kroki:

• Należy na początek dodać repozytorium OpenFOAM do system, tak aby nasz system wiedział skąd ma pobrać aplikację. W tym celu w konsoli wpisujemy:

$ sudo add-apt-repository http://www.openfoam.org/download/ubuntu

• Oprócz dodania repozytorium musimy odświeżyć nasz manager pakietów:

$ sudo apt-get update

• Na koniec możemy już zainstalować samego OpenFOAMa

$ sudo apt-get install openfoam30

OpenFOAM domyślnie powinien zostać zainstalowany w lokalizacji “/opt/openfoam30”.

Oprócz samego OpenFOAMa potrzebujemy także narzędzia do wykonywania postprocessingu. Świetnie nadaje się do tego narzędzie ParaView które domyślnie wspiera wczytywanie siatki i danych wygenerowanych przez OpenFOAMa. Aplikację tą można zainstalować na dwa sposoby: Z repozytorium OpenFOAM (posiada dodatkowe wsparcie do danych OpenFOAMa):

$ sudo apt-get install paraviewopenfoam44

Drugim sposobem jest pobranie ParaView z oficjalnego repozytorium - tutaj wystarczy pobrać archiwum i następnie je rozpakować. Zaletą tego podejścia jest pobranie najnowszej dostępnej wersji tego oprogramowania.

Zadanie

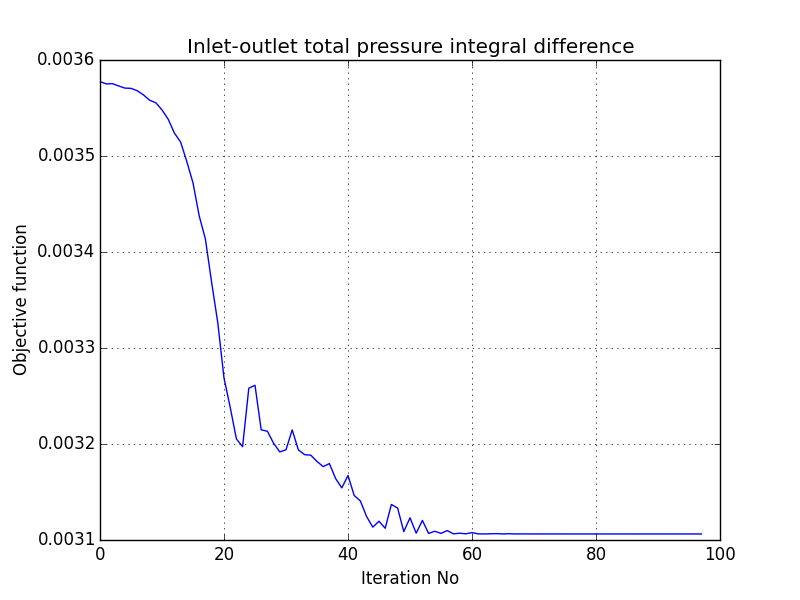
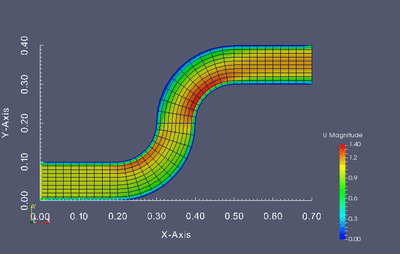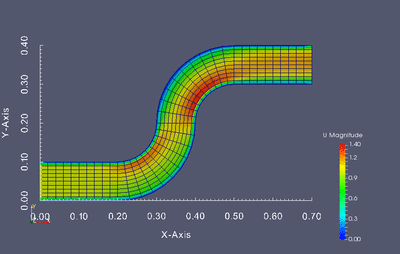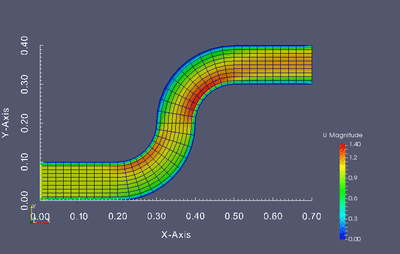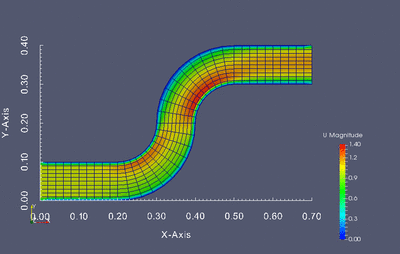
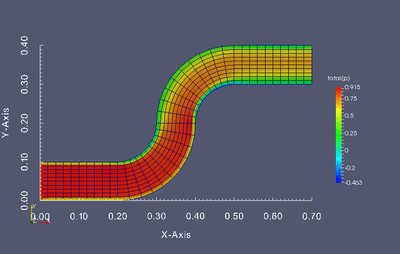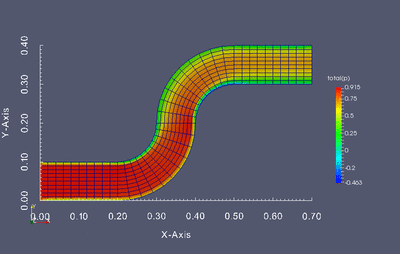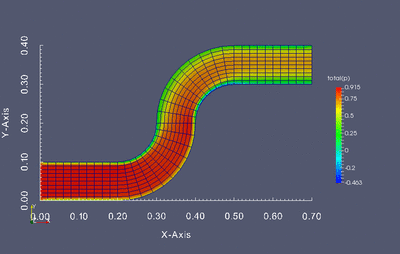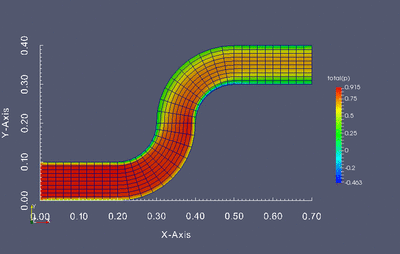
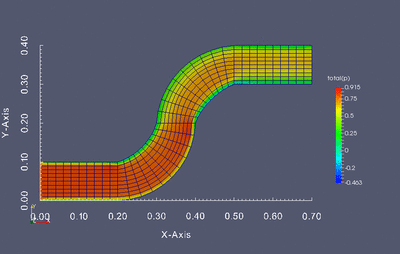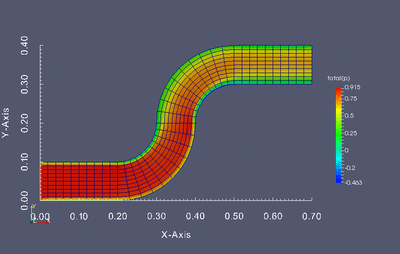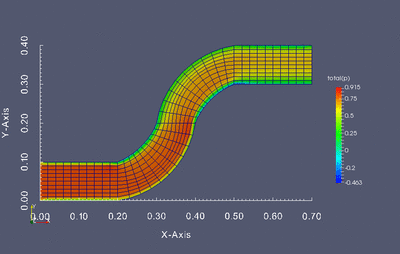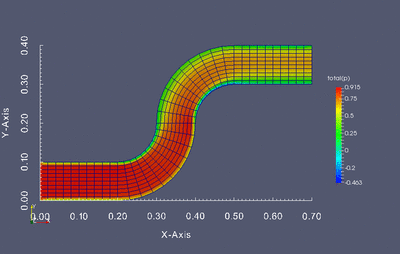
Dokonaj optymalizacji kształtu poniższej geometrii tak aby otrzymany profil kanału zapewniał najmniejszą stratę energii przepływu. Optymalizacji powinny podlegać jednie kolanka kanału, nie wlot i wylot.

kanal

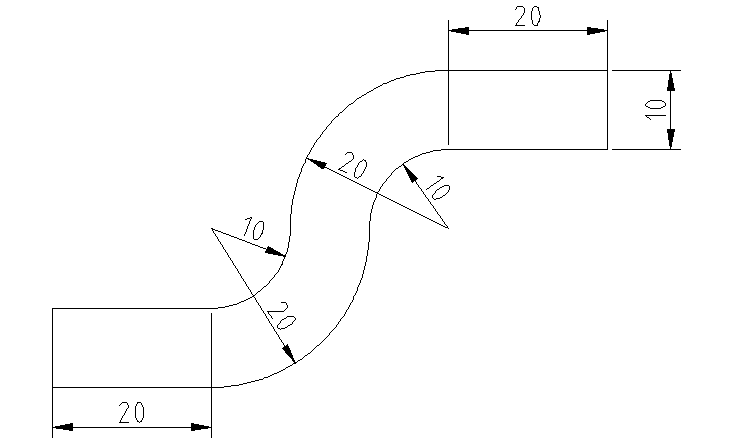
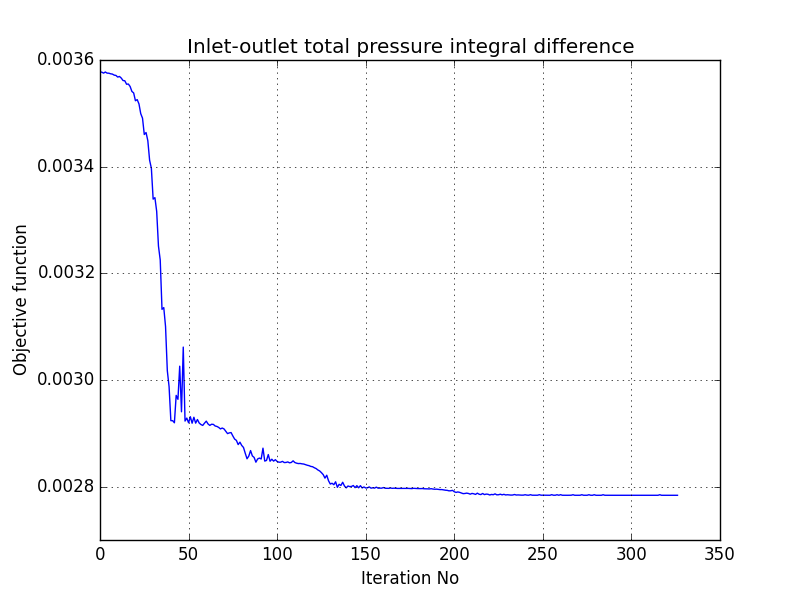
Stratę przepływu można wyznaczyć jako różnicę ciśnienia całkowitego pomiędzy wlotem i wylotem. Twoim zadaniem jest napisanie skryptu w języku Python który będzie służył do modyfikacji siatki obliczeniowej, wczytywania wyników oraz uruchamiania kolejnych symulacji w pętli optymalizacyjnej. W związku z tym kod powinien realizować następujący zadania:

1. Utworzyć bazową siatkę obliczeniową.
2. Wczytywać i zapisywać współrzędne węzłów siatki obliczeniowej z formatu OpenFOAM
3. Wczytywać wyniki z pliku zawierającego obliczone całki z ciśnienia całkowitego na wlocie i wylocie domeny.
4. Uruchamiać symulację
5. Uruchamiać narzędzie minimize z biblioteki scipy.optimize w celu dokonania optymalizacji.

Symulacją i tworzeniem siatki nie należy się przejmować, ponieważ zostały przygotowane specjalne funkcje służące do uruchamiania aplikacji OpenFOAM - znajudują się one w pliku “resources/lab4/of.py”. Aby poprawnie działały te funkcje z poziomu środowiska PyCharm przed jego uruchomieniem należy dodać pewne ścieżki do pliku konfiguracji. W tym celu otwórz plik o nazwie pycharm.sh który znajduje się w folderze bin w miejscu w którym mamy zainstalowanego PyCharma, np.: “/home/wgryglas/Applications/pycharm/bin”.

W pliku tym przed:

# ---------------------------------------------------------------------
# Run the IDE.
# ---------------------------------------------------------------------

dodaj poniższe linijki:

export PYTHONPATH=<ParaView install path>/lib/paraview-4.3/site-packages:<ParaView install path>/lib/paraview-<PV version number>/site-packages/vtk:$PYTHONPATH
export LD_LIBRARY_PATH=<ParaView install path>/lib/paraview-<PV version number>:${LD_LIBRARY_PATH}

zastępując ścieżką do miejsca gdzie jest zainstalowany ParaView na twoim komputerze (sprawdź wpisując komendę which paraview) oraz numerem wersji, np. 4.3 (odczytaj ze ścieżki wyświetlonej komendą which paraview).

Powyższy krok może zostać pominięty, ale w tej sytuacji należało będzie zakomentować funkcje które służą do uruchamiania ParaView “w locie”:

• view
• view2
• saveCurrentImage

Przed rozpoczęciem pracy musimy jeszcze przekopiować folder w którym znajdują się ustawienia OpenFOAMa(ustawienie takie, które zwyczajowo wykonuje się we Fluencie w oknie graficznym) oraz w którym będzie zapisana siatka obliczeniowa oraz wyniki. Folder do przekopiowania znajduje się w “/resources/lab4/channel_optimization”. Powinien on zostać przekopiowany w dowolne miejsce, najlepiej gdzieś poza projektem PyCharm, ponieważ jest to folder symulacji a nie kodu python.

Zadanie to rozwiąż na trzy różne sposoby, które będą różniły się metodą transformacji siatki. #### przypadek a) - dwuparametryczna transformacja siatki

Dokonaj transformacji tak, że parametr określa jak mocno powinny zostać przesunięte węzły względem odległości od linii środkowej kolanka. Parametr dodatni powinien określać odsunięcie od środkowej linii, a ujemny przyciągnięcie do niej. Ponadto transformacja powinna zapewniać, że punkty na skraju kolanka nie zostaną wcale przesunięte (wartość odsunięcia powinna być uzależniona od np. kąta pomiędzy środkiem kolanka a punktem).

optymalizacja dwu parametryczna

optymalizacja 4-parometrowa