Niniejsza instrukcja zawiera ćwiczenia dotyczące arkusza kalkulacyjnego. Można je wykonać wykorzystując darmowe oprogramowanie (np. LibreOffice Calc, OpenOffice Calc czy WPS SpreadSheets lub też komercyjne (np. Microsoft Excel). Składnia formuł we wszystkich wymienionych programach nie różni się znacznie.

Ćwiczenia zostały oparte o program LibreOffice Calc. Dla wygody, każde zadanie można rozwiązać w odrębnej karcie arkusza kalkulacyjnego.

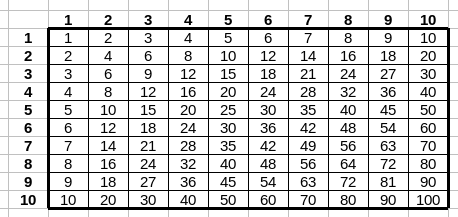
Tabliczka mnożenia

Stwórz tabelę zawierającą tabliczkę mnożenia do dziesięciu. W tym celu:

  • Skorzystaj z możliwości przeciągania formuł.
    Po zaznaczeniu komórki, w jej prawym dolnym rogu pojawi się kwadracik – wystarczy kliknąć w niego i trzymając klawisz myszy przeciągnąć pionowo lub poziomo. Akcja spowoduje skopiowanie formuły i zmianę używanych adresów.
  • Zablokuj wybrane adresy z użyciem symbolu ,,$".
    Przykładowo, odwołanie A$3 oznacza, że przy przeciągnięciu pionowo, numer wiersza nie ulegnie zmianie. Przy przeciągnięciu poziomo, zmianie ulegnie kolumna.
  • W celu sformatowania tabeli zaznacz wybrane komórki, kliknij prawym klawiszem myszki i wybierz Format Cells. Wyświetlone zostaną zakładki umożliwiające zmianę wyglądu tabeli w szerokim zakresie (min. zakładka Borders umożliwia dodanie i edycję linii).

Rys.1. Tabela z tabliczką mnożenia.

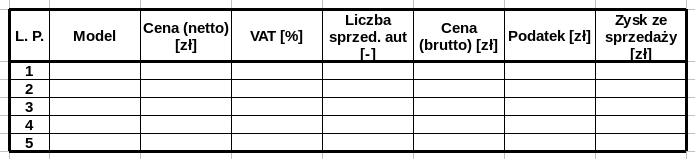
Sprzedaż samochodów

Stwórz tabelę zawierającą informacje o sprzedaży pięciu modeli samochodów.

  • Kolumny \(2\) – \(5\) uzupełnij wymyślonymi danymi.
  • W celu zsumowania zawartości komórek użyj funkcji SUM().
    Argumentem jest zakres komórek, których wartości należy zsumować. Przykładowo SUM(A1:A10) zsumuje wartości w kolumnie A w wierszach od 1 do 10.
  • Tabelę sformatuj tak aby wyglądała jak na Rys. 2.

Rys.2. Tabela sprzedaży aut.

Wyniki z kolokwium

Stwórz dwie tabele. Pierwsza z nich powinna zawierać kolumny o nazwach jak na Rys. 3. Tabelę należy uzupełnić wymyślonymi danymi.

Rys.3. Wyniki z kolokwium.

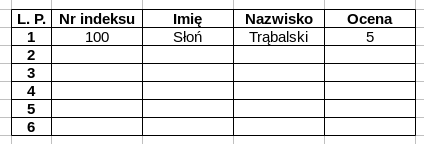
Druga tabela powinna zawierać dwie kolumny: Nr indeksu oraz Imię i Nazwisko.

  • Kolumnę Nr indeksu należy uzupełnić numerami indeksu z poprzedniej tabeli ale w innej kolejności.
  • Kolumnę Imię i Nazwisko należy wypełnić korzystając z funkcji CONCATENATE() i VLOOKUP(). Funkcje można zagnieżdżać, np. wywołanie CONCATENATE(VLOOKUP(...), VLOOKUP(...)) jest prawidłowe.
    Funkcja CONCATENATE() łączy wybrane ciągi znaków w jeden. Przykładowo, formuła CONCATENATE(A1, " ", A2) złączy napisy zawarte w komórkach A1 i A2 wstawiając między nie znak spacji.
    Funkcja VLOOKUP() wyszukuje wiersz zawierający zadaną wartość w pierwszej kolumnie wybranej tabeli i zwraca wartość znajdującą się w wybranej kolumnie. Na przykład, formuła VLOOKUP(A10, A1:D6, 3, 0) wyszuka zawartość komórki A10 w pierwszej kolumnie tabeli A1:D6 i zwróci zawartość odpowiedniego wiersza w trzeciej kolumnie. Ostatni parametr funkcji – zero, oznacza, że pierwsza kolumna tabeli, w której wyszukujemy nie jest posortowana rosnąco.

Wykres funkcji jednej zmiennej

Stwórz wykres funkcji \[ f(x) = \frac{1}{|x - 1| + 1} \] dla \(x \in [-2,2]\).
W tym celu:

  • Utwórz dwie kolumny
    • pierwszą zawierającą wartości argumentu x, dla których ma być narysowany wykres,
    • drugą z wartościami funkcji f(x) (moduł liczby wyznacza funkcja ABS()).
  • Utwórz obiekt typu formuła (Insert -> Object -> Formula w programie OpenOffice) lub obiekt typu Microsoft Equation w celu dodania wzoru funkcji. Tło wzoru możesz zmienić na białe klikając prawym klawiszem myszki na pole i wybierając Area.
  • Zaznacz utworzone kolumny i wybierz Insert -> Chart w celu uruchomienia edytora wykresów. Po utworzeniu wykresu, kliknij na niego dwukrotnie w celu wejścia w tryb edycji poszczególnych elementów wykresu. Sformatuj wykres tak jak na Rys. 4.

Rys.4. Wykres funkcji jednej zmiennej.

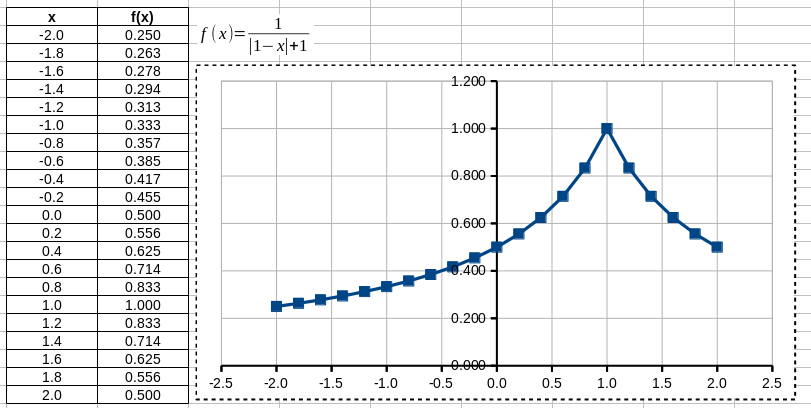
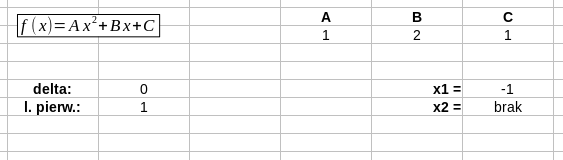
Wyznaczanie pierwiastków funkcji kwadratowej

Utwórz arkusz w celu wyznaczenia pierwiastków funkcji kwadratowej. W tym celu:

  • Dodaj obiekt typu formuła aby zapisać równanie.
  • Wybierz komórki w celu przechowywania współczynników równania i uzupełnij je.
  • Wyznacz wartość delty na podstawie wartości w komórkach odpowiadających współczynnikom.
  • Wyznacz liczbę pierwiastków na podstawie wartości delty. Użyj funkcji IF() w celu sprawdzenia warunków na wartość delty. Przykładowo, formuła IF(A1>0, A2, A3) zwraca zawartość komórki A2 jeśli wartość w komórce A1 jest większa od zera i wartość komórki A3 w przeciwnym przypadku.
  • Wyznacz miejsca zerowe funkcji (formuła SQRT() zwraca pierwiastek kwadratowy z liczby). Uwzględnij przypadek, w którym dany pierwiastek nie istnieje (niech w takim przypadku w komórce wyświetli się napis ,,brak’’).

Rys.5. Miejsca zerowe funkcji kwadratowej.

Importowanie danych z pliku

Ściągnij przykładowy plik wyniki.dat i przenieś go do katalogu z plikiem arkusza kalkulacyjnego. Dane można zaimportować do nowej karty klikając Sheet -> Insert Sheet From File a następnie wybierając plik wyniki.dat. Otworzy się nowe okno, które pozwala wybrać opcje importu. Sekcja Separator Options pozwala wybrać w jaki sposób rozdzielone są dane. Zaznaczamy Space i klikamy OK. Zaimportowane dane często wymagają zmiany separatora dziesiętnego na ten używany w arkuszu. Klikamy Edit -> Find and replace, następnie w polu Find wpisujemy przecinek a w polu Replace kropkę i klikamy Replace All.

Dane są gotowe do dalszej obróbki. Dopasujemy do nich parabolę metodą najmniejszych kwadratów (tzw. linię trendu). W tym celu tworzymy wykres i klikamy na niego dwukrotnie w celu edycji. Następnie wybieramy dowolny punkt (wszystkie punkty powinny się podświetlić na zielono) i z menu głównego wybieramy Insert -> Trend Lines. W zakładce Type wybieramy regresję wielomianową (polynomial) stopnia drugiego, zaznaczamy opcje Show Equation i Show Coefficient of Determination i klikamy OK. Powinniśmy otrzymać wykres podobny do poniższego.

Rys.6. Funkcja trendu.

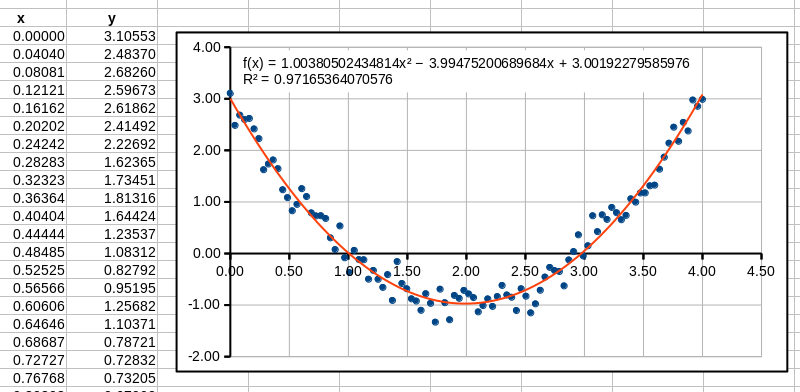
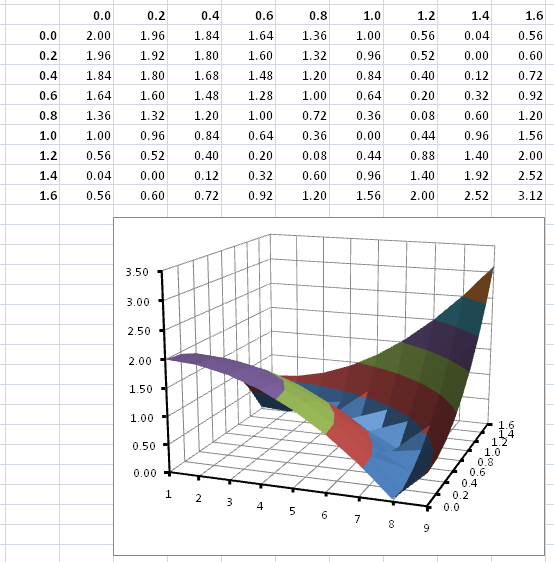
Wykres funkcji dwóch zmiennych (tylko Microsoft Excel)

Utwórz wykres funkcji \[ f(x, y) = |2 - (x^2 + y^2)| \] w obszarze \(D={(x,y)|x\in[0,1.6] \wedge y\in[0,1.6]}\). Pierwszy wiersz powinien zawierać wartości argumentu x a pierwsza kolumna wartości argumentu y. Komórki znajdujące się ,,na przecięciu’’ komórek zawierających współrzędne powinny zawierać wartości funkcji \(f(x,y)\).

Rys.7. Wykres funkcji dwóch zmiennych.