Wstęp
Obliczenia z wykorzystaniem komputerów są nieodłączną częścią współczesnej nauki. Natomiast, podstawą obliczeń komputerowych są obliczenia równoległe. Gdy korzystamy z 1 komputera, nawet bardzo mocnego, jesteśmy ograniczeni do około 32 procesorów (obecnie) i kilkuset Gb pamięci RAM. Co więcej, czas obliczeń spada (przynajmniej tego byśmy sobie życzyli) jak 1/(liczba procesów). Dlatego z reguły potrzebujemy i chcemy wykorzystać ich jak najwięcej.
Obliczenia równoległe
Każdy program przygotowany do pracy równoległej oprócz podstawowego algorytmu, potrzebuje mechanizmu komunikacji. W naszym przypadku będzie to standard MPI czyli Message Passing Interface. Biblioteka OpenMPI dostarcza nam narzędzi niezbędnych do uruchamiania i komunikacji między poszczególnymi procesami składającymi się na nasz “program”.
Ćwiczenie 1
Przygotuj plik program.cpp o poniższej treści. Następnie
skompiluj go za pomocą programu mpic++:
#include <stdio.h>
#include <mpi.h>
#include <unistd.h>
int main(int argc, char *argv[]) {
int numprocs, rank, namelen;
char processor_name[MPI_MAX_PROCESSOR_NAME];
MPI_Init(&argc, &argv);
MPI_Comm_size(MPI_COMM_WORLD, &numprocs);
MPI_Comm_rank(MPI_COMM_WORLD, &rank);
MPI_Get_processor_name(processor_name, &namelen);
printf("Hello World! from process %d out of %d on %s\n",
rank, numprocs, processor_name);
MPI_Finalize();
}Powyższy program można skompilować i uruchomić używając komend:
gdzie 4 to liczba procesorów, na których ma zostać
uruchomiony program.
Przeanalizujmy teraz program. Funkcje MPI_Init i
MPI_Finalize służą do odpowiednio inicjalizacji i
zakonczenia komunikacji pomiedzy procesami. Powinny one być odpowiednio
na początku i na końcu programu, ponieważ tylko pomiedzy nimi można
wykonać jakiekolwiek wywołanie biblioteki MPI i komunikować
się z innymi procesami w grupie. Wywołanie MPI_Comm_size
zwroci nam liczbe procesów (np. 4), zaś
MPI_Comm_rank zwróci nam numer naszego procesu
(np. 0,1,2 lub 3).
Zmienna rank jest wiec jedną z najważniejszych w kodzie,
ponieważ odróżna nasze procesy. Jeśli jej nigdzie nie użyjemy, to
wszystkie nasze procesy zrobią dokładnie to samo.
Ćwiczenie 2
Rozszerz program tak, by każdy proces losował pewne liczby i wypisywał pewne statystyki:
- Zaalokuj tablicę liczb rzeczywistych
ao rozmiarzen = 10000 * (rank + 1) - Wypełnij ją liczbami losowymi z przedziału \([0,1]\)
- Wypisz komunikat o wylosowaniu i wypisz pierwszą liczbę
a[0] - Oblicz \(S_1 = \sum_i a_i\)
- Wyświetl średnią: \(\mu = \frac{1}{n} S_1\)
- Oblicz \(S_2 = \sum_i (a_i - \mu)^2\)
- Wyświetl wariancję: \(\sigma^2 = \frac{1}{n-1} S_2\)
Pamietaj aby we wszystkich komunikatach umieszczać zmienną
rank, tak by było wiadomo, który komunikat pochodzi, od
którego procesu. By mieć pewność, że komunikaty wypisywane są
rzeczywiście wtedy, kiedy występują w kodzie (a nie są buforowane przez
system), dodaj komendę fflush(stdout);
zaraz po każdym wywołaniu printf.
Intrukcja ta powoduje, że cały buforowany tekst zostanie wyświetlony na
ekran od razu.
Aktualnie, losowanie jest bardzo niedoskonałe. Wszystkie procesy
wylosowały ten sam ciąg losowy (można zobaczyć to już po pierwszym
elemencie, który jest identyczny we wszystkich procesach. Żeby tego
uniknąć przekaż np. wartość time(NULL) + rank jako
ziarno do funkcji srand, tak aby ciąg losowy był
zainicjalizowany inną liczbą na każdym procesorze.
Ćwiczenie 3
Zaobserwuj, że różne procesy dochodzą do różnych etapów algorytmu w
różnych momentach. Np. średnia dla procesu 0 może być wyznaczona przed
wypełnieniem liczbami tablicy w procesie 1. Możemy wymusić aby procesy
czekały na siebie nawzajem dodając instrukcję MPI_Barrier(MPI_COMM_WORLD);
po wywołaniach printf/fflush. Bariera w
programach wielowątkowych powoduje, że wszystkie procesy czekają w tym
miejscu kodu, aż reszta procesów dojdzie do tego miejsca, a następnie
wszystkie razem ruszają dalej. Zauważ, że powoduje to iż program działa
tak wolno, jak jego najwolniejszy element. Przebieg programu we
wszystkich procesach jest pokazany poglądowo na poniższym obrazku:
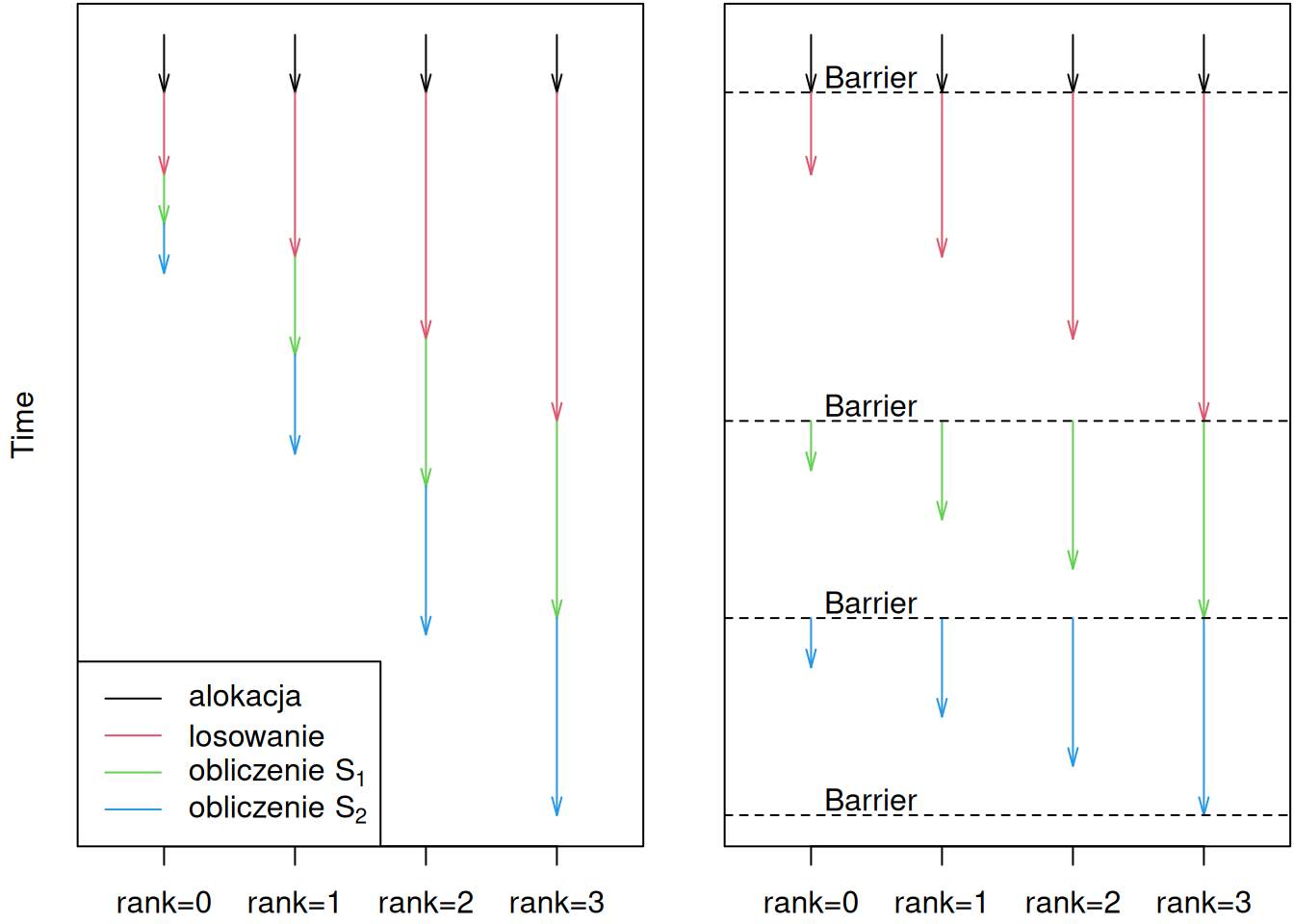
Ćwiczenie 4
Użyj funkcji wykonującej redukcję aby obliczyć średnią globalną (po wszystkich procesach) i wariancję z \(a\). Redukcja w programowaniu równoległym polega na wykonaniu jakiejś operacji, np. sumowania czy wzięcia maxiumum, na danych ze wszystkich procesów. W bibliotece MPI mamy do dyspozycji funkcję:
sourceto wskaźnik do danych, które mamy np. zsumować.destinationto wskaźnik do miejsca, gdzie ma być umieszczony wynik.countto liczba elementów danych do zsumowania. Czyli np.1jeśli dane to jedna liczba.datatypeto typ danych, które sumujemy:MPI_INTlubMPI_DOUBLE.operationto operacja, którą wykonujemy, np:MPI_SUMlubMPI_MAX.rootto numer procesu, do którego przesyłamy wynik, np:0.- Ostatni argument to uchwyt komunikatora, na którym ma zostać
wykonana redukcja. W naszym wypadku to domyślny komunikator
MPI_COMM_WORLD
Użyj tej funkcji aby obliczyć globalne statystyki, a następnie
wyświetl je (pamietaj, że mają one sens tylko na węźle
root). Weź pod uwagę, że globalne n jest inne
niż n lokalne.
Bliźniaczą do funkcji MPI_Reduce jest funkcja
MPI_Allreduce. Przesyła ona wynik do wszystkich procesów, a
nie tylko do procesu root.
Ćwiczenie *
Stwórz nowy program równoległy program2.cpp, który
będzie obliczał powyższą średnią i wariancję, używając tylko jednej
pętli, bez alokowania tablicy a (tzn., będzie liczył
średnią i wariancję bez przechowywania pojedyńczych elementów). By to
zrobić przekształć wzór na wariancję:
\(\sigma^2 = \frac{1}{n-1}\sum_i\left(a_i - \frac{1}{n}\sum_j a_j\right)^2\)
tak aby był wyrażony za pomocą \(S_1\) i nowego \(\hat S_2 = \sum_i a_i^2\), który da się
obliczyć bez znajomości średniej \(\mu\). Użyj we wszystkich procesach tego
samego (bardzo wysokiego) n. Porównaj czas wykonania
wykonując:
Kolejka PBS
W przypadku każdego dużego systemu komputerowego potrzebny jest jakiś
mechanizm zarządzania zasobami: 2 osoby nie mogą naraz korzystać z tego
samego procesora/rdzenia. W prawdziwym systemie komputer centralny służy
do zlecania zadań, pozostałe, tzw. węzły obliczeniowe, przyjmują i
wykonują zadania. Na info3 jest tylko jeden węzeł który
spełnia obie role.
Ćwiczenia
Sprawdź co zrobi komenda qsub -I
(wielka litera i). To program do wysyłania zadań do wykonania. Opcja
-I oznacza tryb interaktywny: zostaniemy zalogowani na
wolny węzeł przez ssh. Wpisz teraz qstat, sprawdź opcje
-n i -f. Zobacz, że twoje ‘zadanie’ jest
uruchomione w kolejce. Wyloguj się teraz, bo blokujesz zasoby kolejki.
Jednocześnie mogą być wykorzystywane tylko 4 rdzenie. Ilością
pobieranych zasobów można sterować poprzez flagę -l,
np.:
Parametr walltime=00:00:10 mówi nam o maksymalnym czasie
trwania zadania. Po upłynięciu tego czasu zadanie zostanie automatycznie
przerwane.
Zadania nieinteraktywne
W większości przypadków czas trwania zadania interaktywnego jest
mocno ograniczony. Bardziej użyteczne są zadania nieinteraktywne. Aby
zlecić takie zadanie potrzebny jest nam plik zadania
plik.sh:
Zlecamy jego wykonanie przez
Obejrzyj zawartość katalogu, znajdź pliki o rozszerzeniu
.oXX i .eXX. Czym one są? Dodaj do skryptu
plik.sh komendę sleep 8, która
spowoduje ze zadanie zaśnie na 8 sekund, tak by w liście
wypisywanej przez qstat dało się je zobaczyć. Jako grupa
możecie dodać wiele takich zadań i zobaczyć jak są po kolei realizowane
przez kolejkę PBS.
Ćwiczenie
Spróbuj wykonać któryś z wcześniejszych skryptów konwerujących obrazki (np konwersje .jpg na .gif) jako nieinteraktywne zadanie w kolejce.