Interpolacja
Pliki do wykorzystania w poniższym ćwiczeniu można pobrać za pomocą poniższych linków:
1. Interpolacja w praktyce inżynierskiej
Dziś będziemy się zajmować zagadnieniem interpolacji. Załóżmy, że w pewnym urządzeniu technicznym ze zbiornika, który może być umieszczony na różnej wysokości, rurą wypływa woda aż do jego opróżnienia. Wykonaliśmy eksperyment, umieszczając rzeczony zbiornik na kilku różnych wysokościach (np. 2, 3 i 4 m) i dla każdej z tych wysokości dokonaliśmy pomiaru czasu, po jakim następuje opróżnienie zbiornika. W procesie projektowania (może optymalizacji?) zależy nam zwykle na tym, aby umieć przewidzieć czas opróżniania dla dowolnej wysokości umieszczenia zbiornika. Wysokość ta zawiera się między ustalonymi wartościami skrajnymi, a więc np. na wysokości wynoszącej 3.27 m. Musimy więc przez nasze dane pomiarowe umieć przeprowadzić krzywą, która wiarygodnie przybliży taką zależność. Mówimy wtedy o interpolacji, czyli interpolowaniu zbioru dyskretnych (punktowych) danych w ciągłą zależność określoną dla każdego argumentu leżącego między skrajnymi punktami, na których opieramy interpolację.
Meritum
Interpolacja to zagadnienie przeprowadzenia krzywej (pewnej zależności) przez wszystkie punkty ze zbioru danych tak, aby otrzymać przebieg domniemanej zależności między punktami pomiarowymi. Liczba stopni swobody dopasowanej krzywej musi być równa liczbie punktów w zbiorze danych (liczba równań musi być równa liczbie niewiadomych).
2. Interpolacja wielomianowa
W tym momencie przejdziemy do zagadnienia interpolacji wielomianowej Lagrange’a. Funkcja interpolująca to wielomian postaci: \[ w(x) = \sum_{i=0}^{n} y_i \prod_{j=0 \land j\neq i}^{n} \frac{x - x_j}{x_i - x_j} \] gdzie \((x_i, y_i)\) to punkt pomiarowy.
Ćwiczenia
- Napisz program, który wygeneruje zestaw n punktów (będących punktami
eksperymentalnymi) o współrzędnych: \[
\left( x_i, \exp(-x_i^2) \right)
\] gdzie \[
x_i = a + i \cdot h
\] \[
h = \frac{b - a}{n-1}
\] \[
i = 0, \ldots n-1
\] zaś \(a = -2.0\) i \(b = 2.0\).
Przypomnienie: użycie funkcjimallocdo alokacji pamięci:
double *x;
x = (double *) malloc(n * sizeof(double));
if (x == NULL) {
fprintf(stderr, "malloc: can not allocate x.\n");
exit(1);
}
/* operacje z wykorzystaniem tablicy x */
free(x);- Oblicz wartość wielomianu interpolacyjnego Lagrange’a w punktach
rozmieszczonych czterokrotnie gęściej, tzn. o współrzędnych: \[
t_i = a + i \cdot \frac{h}{4}, \; i = 0, \ldots 4n - 4.
\] Wartość funkcji w dowolnie wybranym punkcie \(t_i\) oblicz, korzystając z funkcji
lagrange(double *x, double *y, int n, double xx).
Parametry funkcji oznaczają:
x,y- wskaźniki do n-elementowych tablic zawierających współrzędne punktów interpolowanych,n- długość wektora (liczba jego elementów),xx- bieżąca wartość argumentu (zmienna rzeczywista), dla którego obliczamy wartość wielomianu Lagrange’a. Przykład najprostszego użycia funkcjilagrangepokazany jest poniżej:
int main() {
double x[3] = {0, 1, 2};
double y[3] = {0, 1, 4};
double f, t = 1.5
/* Wyznacz wartosc paraboli dla t = 1.5 */
f = lagrange(x, y, 3, t);
}- Wydrukuj uzyskane wyniki (dla każdego \(t_i\)) na ekran.
- Wyświetl je graficznie, korzystając z funkcji
scale(double x0, double y0, double x1, double y1)zaimplementowanej w bibliotece graficznej. Kod poniżej pokazuje prosty przykład wyświetlenia wykresu funkcji sinus.
int main() {
double pi = 4. * atan(1.);
graphics(600, 400);
scale(0, -1.2, 7, 1.2); // xmin = 0, ymin = -1.2, x_max = 7, ymax = 1.2
double x = 0;
while(x < 2 * pi) {
point(x, sin(x));
x += 0.01;
}
wait();
}- Obejrzyj wyniki na wykresie dla różnych wartości parametru \(n\).
- Zapisz wyniki do pliku.
- Dla wybranego \(n\) stwórz w arkuszu kalkulacyjnym wykres błędu interpolacji.
- Powtórz wyniki dla innej funkcji interpolowanej. Przyjrzyj się dokładnie wynikom otrzymanym dla funkcji \(|x|\). Dlaczego tak wyglądają?
3. Dla ambitnych
Sprawdźmy czy można coś zrobić, aby poprawić zachowanie i stabilność interpolacji wielomianowej. Posłużymy się w tym celu dalej funkcją \(|x|\) jako jedną z bardziej wymagających.
Węzły Czebyszewa
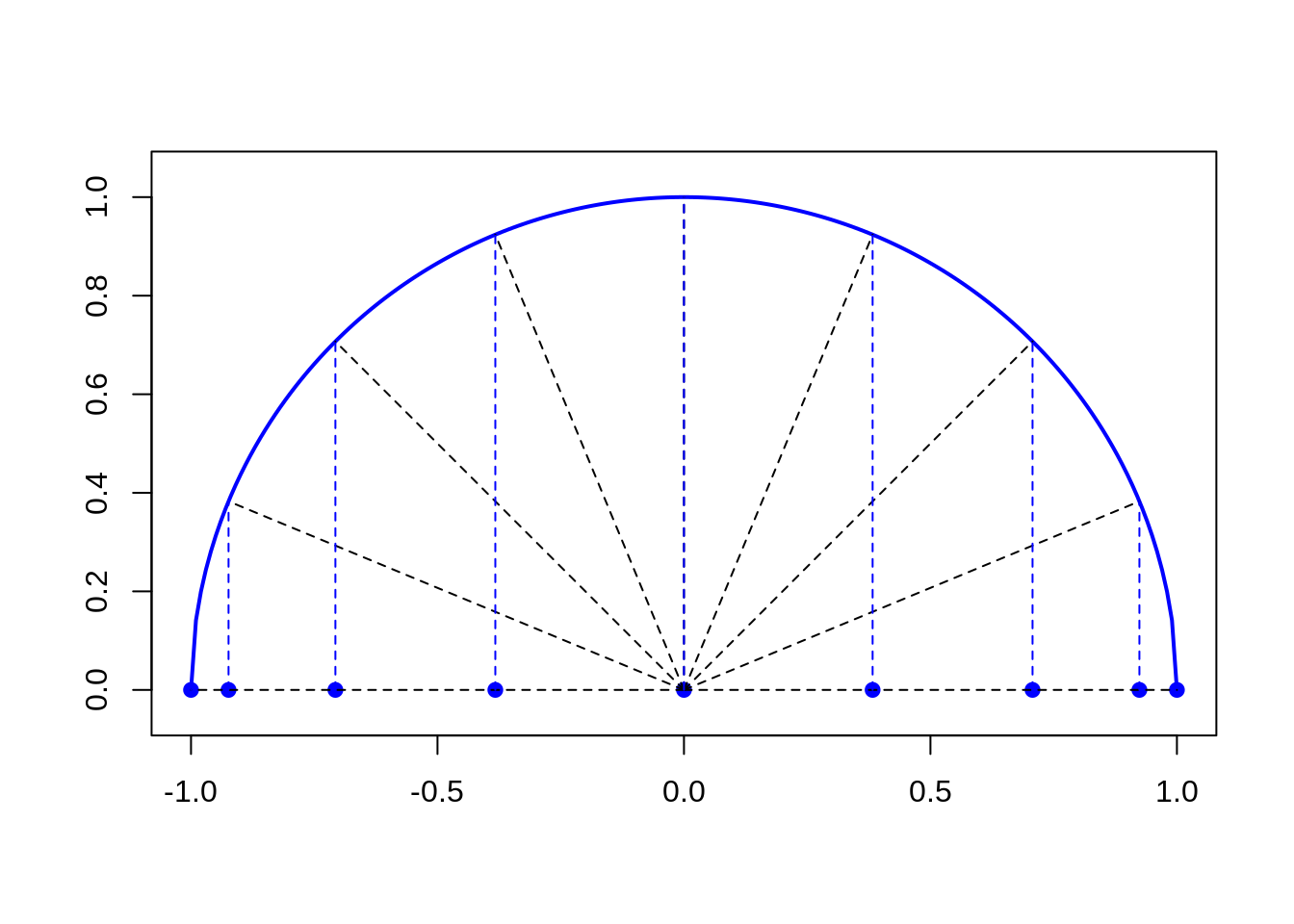
Spróbujmy oprzeć naszą interpolację na punktach, których odcięte będą dobrane w odpowiedni sposób. Do tej pory punkty były rozłożone równomiernie. Teraz rozłóżmy je w taki sposób, aby były gęściej rozłożone przy brzegach obszaru i rzadziej w środku. Można tego dokonać następująco. Chcemy rozłożyć punkty w przedziale \(x = [-1, 1]\). Wykreślmy zatem półokrąg o środku w połowie tego przedziału i promieniu równym połowie długości przedziału (czyli u nas półokrąg o środku w \(x = 0\) i promieniu \(R = 1\)). Podzielmy łuk równomiernie (mierząc wzdłuż łuku) na \(n - 1\) fragmentów. Teraz dokonajmy rzutowania punktów podziału na oś \(x\). Tak wygenerowane węzły mają więc współrzędne (wyprowadź w domu ten wzór) na osi \(x\) dane wzorem: \[ x_i = -\cos\left( \frac{i \cdot \pi}{n-1} \right), \; i = 0, \ldots n - 1 \] Dla ogólnego przypadku przedziału \(x = [a, b]\) wzór wyglądałby tak: \[ x_i = -\frac{b-a}{2} \cos\left( \frac{i \cdot \pi}{n-1} \right) + \frac{a+b}{2}, \; i = 0, \ldots n - 1 \]
Ćwiczenie
Zmodyfikuj swój program tak, aby początkowy zestaw punktów generowany był dla współrzędnych zdefiniowanych w powyższy sposób. Sprawdź działanie interpolacji funkcji \(|x|\) z użyciem węzłów Czebyszewa. Czy wyniki są inne?